

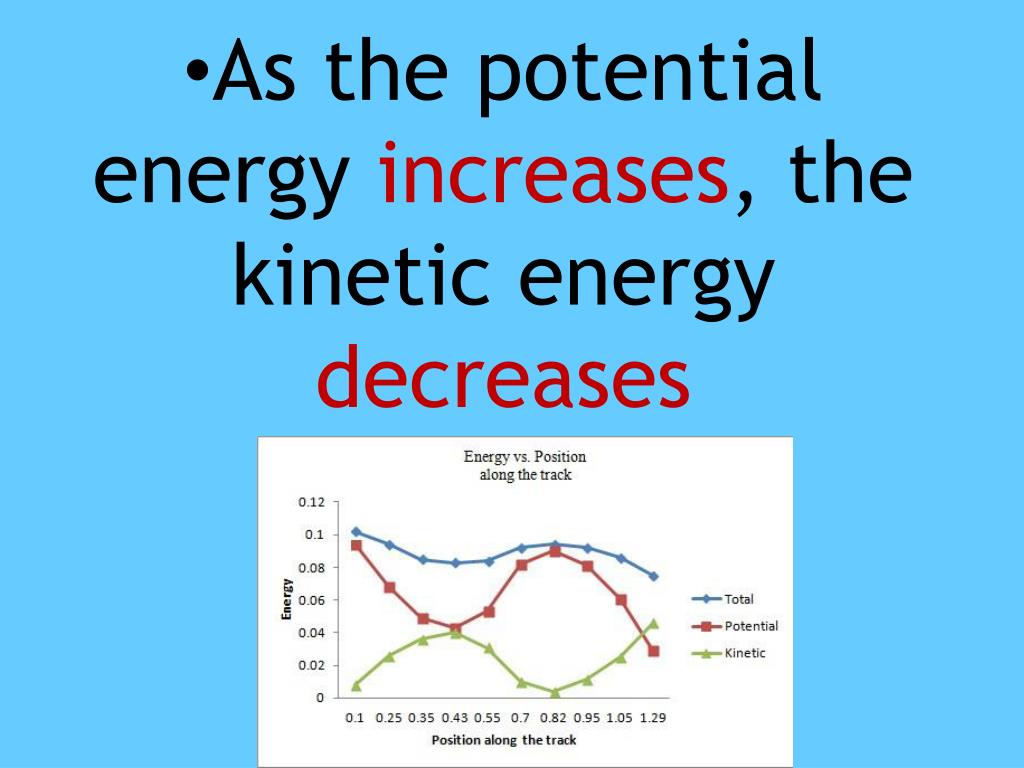
In a radial field, all vectors either point directly toward or directly away from the origin. Radial fields model certain gravitational fields and energy source fields, and rotational fields model the movement of a fluid in a vortex. There are two types of vector fields in \(ℝ^2\) on which this chapter focuses: radial fields and rotational fields. Instead, we can choose points at the intersections of grid lines and plot a sample of several vectors from each quadrant of a rectangular coordinate system in \(ℝ^2\). If we were to plot the image vector at each point in the region, it would fill the region completely and is useless. We should plot enough vectors to see the general shape, but not so many that the sketch becomes a jumbled mess. For example, suppose the vector associated with point \((4,−1)\) is \(⟨3,1⟩\). To do this, draw the vector associated with a given point at the point in a plane. Although the direction and relative intensity of the electric field can be deduced from a set of field lines, the lines can also be misleading. The direction of electric field lines from a charge will depend on the nature of the charge if the charge is positive it will be directed away from the charge. This is because electric potential is the work done against the direction of electric. Note that the potential is greatest (most. Since we cannot represent four-dimensional space visually, we instead draw vector fields in \(ℝ^2\) in a plane itself. In the direction of electric field the electric potential decreases. The equipotential lines can be drawn by making them perpendicular to the electric field lines, if those are known. c) It's kinetic energy will decrease since potential energy is increasing d) its total energy is staying the same. b) It's electric potential energy will decrease since it is going in the opposite direction as the electric field lines. Therefore the “graph” of a vector field in \(ℝ^2\) lives in four-dimensional space. a) the electric potential will increase since an electron goes the opposite way as the proton. We can now represent a vector field in terms of its components of functions or unit vectors, but representing it visually by sketching it is more complex because the domain of a vector field is in \(ℝ^2\), as is the range. In this section, we study vector fields in \(ℝ^2\) and \(ℝ^3\). Intuitively, a vector field is a map of vectors. The speed of the water increases, and a whirlpool occurs in part of the rapids.Įach figure illustrates an example of a vector field. As the water moves from left to right, it encounters some rapids around a rock. Since the vectors to the left of the figure are small in magnitude, the water is flowing slowly on that part of the surface. The vector associated with a given point on the river’s surface gives the velocity of the water at that point. \) shows the velocity of a river at points on its surface.


 0 kommentar(er)
0 kommentar(er)
